黑鱼的池塘

1 介绍

1.1 定义

• 表示“多对多”的关系
• 包含：
  1. 一组顶点：通常用V(Vertex)表示顶点集合
  2. 一组边：通常用E(Edge)表示边的集合：无向边$(v,w)\in E, 其中 v,w\in V$；有向边$<v,w>$表示从v到w的边；不考虑重边和自会路

1.2 常见术语

• 无向图：所有的边都没有方向的图
• 有向图：边是有方向的
• 网络：边带权重的图
• 度：从顶点发出的边数为“出度”，指向该点的边数为“入度”
• 连通：如果从V到W存在一条(无向)路径，则称V和W是连通的
• 路径：V到W的路径是一系列顶点$\{V, v_1, v_2, ..., v_n, W\}$的集合，其中任一对相邻的顶点间都有图的边。路径的长度是路径中的边数（如果带权，则是所有边的权重和）。如果V到W之间的所有顶点都不同，则称为简单路径
• 回路：起点等于终点的路径
• 连通图：图中任意两顶点均连通
• 连通分量：无向图的极大连通子图，极大表示：①顶点数极大，再加上一个顶点就不连通了。②边数极大，包含子图中的所有顶点相连的所有边。
• 强连通：有向图中顶点V和W之间存在双向路径，则称V和W是强连通的
• 强连通图：有向图中任意两个顶点均强连通
• 强连通分量：有向图中的极大强连通子图

1.3 图的表示

1.3.1 邻接矩阵

1. 邻接矩阵G[N][N]——N个顶点从0到N-1编号

$G[i][j]=\begin{cases} 1& 若<v_i,v_j>是G中的边\\ 0& 否则 \end{cases}$

2. 邻接矩阵的特点：
   • 直观、简单、好理解
   • 方便检查任意一对顶点间是否存在边
   • 方便找任一顶点的所有“邻接点”（有边直接相连的顶点）
   • 方便计算任一顶点的“度”
3. 邻接矩阵的缺点：
   • 浪费空间————存稀疏图（点很多而边很少）有大量无效元素，但存稠密图（特别是完全图）挺合算
   • 浪费时间————统计稀疏图中一共有多少条边

1.3.2 邻接表

1. 邻接表：G[N]为指针数组，数组的每个元素存放一行链表的头结点，只存非0元素
   
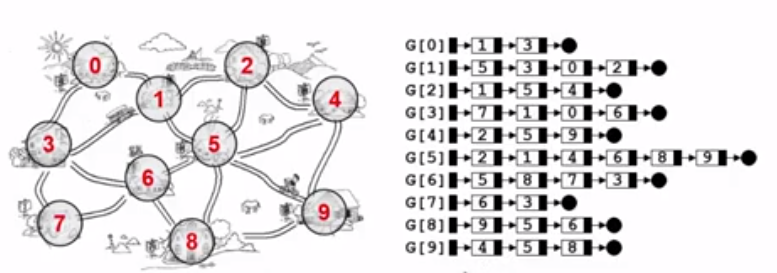
2. 邻接表的特点：
   • 方便找任一顶点中的所有“邻接点”
   • 节约稀疏图的空间（需要N个头指针+2E个结点，E为边数）
   • 方便计算无向图的度和有向图的出度，但不方便计算有向图的入度
3. 邻接表的缺点
   • 本身多了一个指针域，表示网络来说，多了一个权重域，所以仅适用于表达稀疏图
   • 不方便计算有向图的入度（除非再构造一个“逆邻接表”）

1.4 图的遍历

1.4.1 深度优先遍历（Depth Fisrt Search，DFS）

/* 伪代码 */
void DFS(Vertex V){
    visited[V] = true;
    for(V的每个邻接点W)
        if(!visited[W])
            DFS(W);
}

• 用邻接表存储图，时间复杂度为$O(N+E)$ (N为结点数，E为边数)
• 用邻接矩阵存储图，时间复杂度为$O(N^2)$

1.4.2 广度优先遍历（Breadth Fisrt Search，BFS）

/* 伪代码 */
void BFS(Vertex V){
    visited[V] = true;
    Enqueue(V, Q);
    while(!IsEmpty(Q)){
        V = Dequeue(Q);
        for(V的每个邻接点W){
            if(!visited[W]){
                visited[W] = true;
                Enqueue(V, Q);
            }
        }
    }
}

• 用邻接表存储图，时间复杂度为$O(N+E)$ (N为结点数，E为边数)
• 用邻接矩阵存储图，时间复杂度为$O(N^2)$

2 最短路径

2.1 定义

• 最短路径：在网络中，求两个顶点间的所有路径中，边权值之和最小的那条路径就是这两点间的最短路径。
• 源点：求最短路径时的起点称之为源点
• 终点：求最短路径时的终点称之为终点
• 单源最短路径问题：从某固定源点出发，求其到所有其他顶点的最短路径
• 多源最短路径问题：求任意两顶点间的最短路径

2.2 方法

2.2.1 无权图的单源最短路算法

// T = O(|V|+|E|)
void Unweighted( Vertex S ){
    Enqueue(S, Q);
    while(!IsEmpty(Q)){
        V = Dequeue(Q);
        for(V的每个邻接点W){
            if(dist[W]==-1){
                dist[W] = dist[V]+1;
                path[W] = V;
                Enqueue(W, Q);
            }
        }
    }
}

2.2.2 有权图的单源最短路算法——Dijkstra算法

• 令$S=\{源点s+已经确定了最短路径的顶点v_i\}$
• 对任一未收录的顶点v，定义dist[V]为s到v的最短路径长度，但该路径仅经过S中的顶点。即路径$\{s\rightarrow (v_i \in S)\rightarrow v\}$的最小长度
• 真正的最短路径只经过S中的顶点
• 每次从未收录的顶点中选一个dist最小的收录（贪心）：如果采用遍历的方式获得dist最小，则$T=O(|V|^2+|E|)$；如果采用最小堆的方法建立和获得最小dist，则$T=O(|V|log(|V|)+|E|log(|V|))=O(|E|log(|V|))$
• 增加一个v到S，可能影响另外一个w的dist值

void Dijkstra(Vertex S){
    while(1){
        V = 未收录顶点中dist最小者;
        if(V不存在)
            break;
        collected[V] = true;
        for(V的每个邻接点W){
            if(collected[W] = false){
                if(dist[V]+E<v,w> < dist[W]){
                    dist[W] = dist[V]+E<v,w>;
                    path[W] = V;
                }
            }
        }
    }
}

2.2.3 多源最短路算法——Floyd算法

• $D^k[i][j]=路径\{i \rightarrow \{l\le k\}\rightarrow j\}$
• $D^0, D^1, ..., D^{|v|-1}[i][j]$即给出了从0到|v|-1逐次加入顶点后i到j的最短距离矩阵
• $D^{-1}$应为带权的邻接矩阵，对角线为0
• 当$D^{k-1}$已经完成，递推到$D^k$时：如果新加入的顶点k不影响$D^{k-1}$各个顶点彼此间最短路径，则不需要更新；反之，如果影响了，那么影响后的最短路径必然由两段最短路径组成，即$D^k[i][j]=D^{k-1}[i][k]+D^{k-1}[k][j]$

void Floyd(){
    for(i=0;i<N;i++){
        for(j=0;j<n;j++){
            D[i][j] = G[i][j];
            path[i][j] = -1;
        }
    }
    for(k=0;k<N;k++)
        for(i=0;i<N;i++){
            for(j=0;j<n;j++)
                if(D[i][k]+D[k][j]<D[i][j]){
                    D[i][j] = D[i][k]+D[k][j];
                    path[i][j] = k;
                }
            }
}

3 最小生成树

3.1 定义

• 是一棵无回路的树，|V|个顶点一定有|V|-1条边
• 包含了全部的顶点，|V|-1条边都在路里
• |V|-1条边的权重和最小

3.2 方法

3.2.1 Prim算法

void Prim(Vertex s){
    MST = {s};
    while(1){
        v = 未收录顶点中dist最小的;
        if(这样的V不存在)
            break;
        将V收录进MST: dist[v] = 0;
        for(v的每个邻接点W){
            if(W未被收录)
                if(E<v,w> < dist[w]){
                    dist[W] = E<v,w>;
                }
        }
    }
}

3.2.2 Kruskal算法——将森林合并成树

• 思路：从图中每次找到边权值最小的边，如果该边不构成回路，则加入到生成树集合；如果构成，删除掉该边
• $T=O(|E|log(|E|))$

void Kruskal(Vertex s){
    MST = {};
    while(MST中的边不到|V|-1条&&E中还有边){
        e=E中权重最小的边；            /* 最小堆 */
        Delete(E, e); 
        if(e加入到MST没有构成最小回路)  /* 并查集 */
            e 加入到 MST;
    }
    if( MST中的边不到|V|-1条 )
        Error("生成树不存在")
}